题目：
假设有一棵完全二叉树（Complete Binary Tree），它一共有 1001 个节点。请问这棵二叉树中，叶子节点（度为 0 的节点）共有多少个？
答案：
501个
解析：
这是一个经典的二叉树性质问题。我们可以通过二叉树的通用性质来计算，而不需要考虑它是否为“完全二叉树”（完全二叉树的条件主要用于确定树的形态，但在节点度数关系上，所有二叉树遵循相同的公式）。
计算过程：
1. 定义变量：
·设 
为总节点数，已知 
。
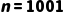·设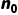 
为叶子节点（度为 0）的个数。
·设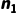 
为度为 1 的节点个数。
·设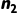 
为度为 2 的节点个数。
2. 利用二叉树的两个基本性质：
·性质 1（节点总数）：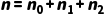
·性质 2（边数关系）： 在任何树中，边数等于节点总数减 1。在二叉树中，边是由度为 1 和度为 2 的节点发出的，即：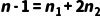
3. 推导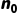 
和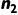 
的关系：将性质 1 代入性质 2： 
消去两边的 
： 
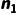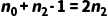得出：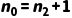
（即叶子节点数总是比度为 2 的节点数多 1 个）。
4. 结合完全二叉树的特有性质：在完全二叉树中，度为 1 的节点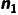 
只有两种可能：0 个或 1 个。 我们将 
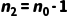代入总数公式：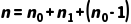 
5. 确定结果：
·如果 
：
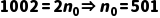
·如果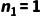 
：
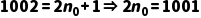（无整数解，舍去）
结论：
这棵二叉树中，叶子节点共有 501 个。
快速简便方法：
对于完全二叉树，如果总节点数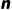 
是奇数，则叶子节点数 
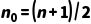。 计算：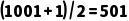
。
原创不易，希望对你有帮助
“点赞”与“❤️”，考研稳上岸～
